8. Properties of Curves
c. Velocity, Acceleration, and Jerk
Given a space curve, \(\vec{r}(t)\), its velocity, acceleration, and jerk are defined exactly as they were for functions of one variable. They are the first, second and third derivatives of the position:
The position is:
\(\vec{r}(t)\)
The velocity is:
\(\vec{v}(t)=\dfrac{d\vec{r}}{dt}\)
The acceleration is:
\(\vec{a}(t)=\dfrac{d\vec{v}}{dt}=
\dfrac{d^2\vec{r}}{dt^2}\)
The jerk is:
\(\vec{j}(t)=\dfrac{d\vec{a}}{dt}=\dfrac{d^{3}\vec{r}}{dt^{3}}\)
Velocity
On the previous page, we defined the velocity, \(\vec{v}\), to be the derivative of the position and we saw that it is tangent to the curve. Consequently, we defined the tangent vector to be the velocity vector.
The quartic function at the right is: \[ y=1+\dfrac{2}{5}x^2+\dfrac{1}{20}x^3-\,\dfrac{1}{60}x^4 \] It may be parametrized as the position vector: \[ \vec{r}(t) =\left(t,1+\dfrac{2}{5}t^2+\dfrac{1}{20}t^3-\,\dfrac{1}{60}t^4 \right) \] To find the velocity vector, we simply take the derivative as \[ \vec{v}(t)=\dfrac{d\vec{r}}{dt} =\left\langle \dfrac{dx}{dt},\dfrac{dy}{dt}\right\rangle =\left\langle 1,\dfrac{4}{5}t+\dfrac{3}{20}t^2-\,\dfrac{1}{15}t^3\right\rangle \]
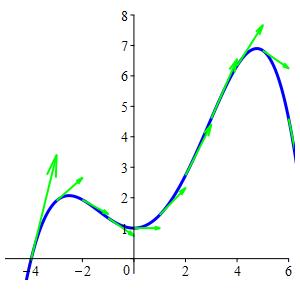
\(\vec{v}(t)\) is Green
Acceleration
Since the acceleration is the derivative of the velocity, it measures the change of both the magnitude and the direction of the velocity. We will see later in this chapter that the change in the magnitude of the velocity is measured by the projection of the acceleration along the velocity (the tangential acceleration \(a_{T}=\text{comp}_{\vec v}\vec a\)) while the change in the direction of the velocity is measured by the projection of the acceleration perpendicular to the velocity (the normal acceleration \(a_{N}=\text{comp}_{\perp\vec v}\vec a\)). (See the definitions of scalar projections.)
For the quartic curve: \[ \vec{r}(t) =\left(t,1+\dfrac{2}{5}t^2+\dfrac{1}{20}t^3-\,\dfrac{1}{60}t^4\right) \] we have already found the velocity vector: \[ \vec{v}(t) =\left\langle 1,\dfrac{4}{5}t+\dfrac{3}{20}t^2-\,\dfrac{1}{15}t^3\right\rangle \] To find the acceleration vector, we simply take another derivative: \[ \vec{a}(t)=\dfrac{d\vec{v}}{dt} =\left\langle 0,\dfrac{4}{5}+\dfrac{3}{10}t-\,\dfrac{1}{5}t^2\right\rangle \]
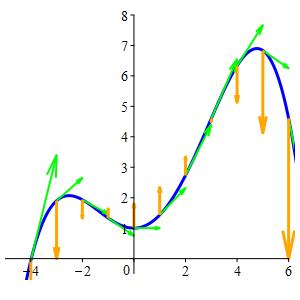
\(\vec{v}(t)\) is Green
\(\vec{a}(t)\) is Orange
Jerk
Jerk is the rate of change of acceleration. It only appears in one place in this book, in a formula for the torsion of a parametric curve.
For the quartic curve: \[ \vec{r}(t) =\left(t,1+\dfrac{2}{5}t^2+\dfrac{1}{20}t^3-\,\dfrac{1}{60}t^4 \right) \] we have already found the acceleration vector: \[ \vec{a}(t)=\dfrac{d\vec{v}}{dt} =\left\langle 0,\dfrac{4}{5}+\dfrac{3}{10}t-\,\dfrac{1}{5}t^2\right\rangle \] To find the jerk vector, we simply take the derivative again: \[ \vec\jmath(t)=\dfrac{d\vec{a}}{dt} =\left\langle 0,\dfrac{3}{10}-\,\dfrac{2}{5}t\right\rangle \]
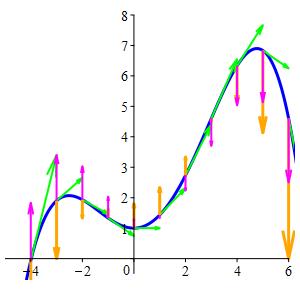
\(\vec{v}(t)\) is Green
\(\vec{a}(t)\) is Orange
\(\vec\jmath(t)\) is Magenta
Caution: Be careful not to confuse the jerk, \(\vec\jmath\), with the basis unit vector in the \(y\) direction, \(\hat\jmath\). The context will always make it clear which quantity is being referred to. Additionally, jerk is always written with a vector sign, \(\vec\jmath\), while the basis unit vector is written with a hat, \(\hat{\jmath}\).
Note that the interpretations of velocity, acceleration, and jerk we have arrived at here are similar to the ones used in Single Variable Calculus. The difference is that now we are dealing with vector quantities as opposed to scalar quantities.
Calculate the velocity, acceleration, and jerk for the Circle \(\vec{r}(\theta)=\left\langle4\cos(\theta),4\sin(\theta),2\right\rangle\).
Position:
\(\vec{r}(\theta)
=(4\cos\theta,4\sin\theta,2)\)
Velocity:
\(\vec{v}(\theta)=\dfrac{d\vec{r}}{d\theta}
=\langle -4\sin\theta,4\cos\theta,0\rangle\)
Acceleration:
\(\vec{a}(\theta)=\dfrac{d\vec{v}}{d\theta}
=\langle -4\cos\theta,-4\sin\theta,0\rangle\)
Jerk:
\(\vec\jmath(\theta)=\dfrac{d\vec{a}}{d\theta}
=\langle 4\sin\theta,-4\cos\theta,0\rangle\)
The position is:
\[
\vec{r}(\theta)=(4\cos\theta,4\sin\theta,2)
\]
We simply differentiate three times:
The velocity is:
\[
\vec{v}(\theta)=\dfrac{d\vec{r}}{d\theta}
=\langle -4\sin\theta,4\cos\theta,0\rangle
\]
The acceleration is:
\[
\vec{a}(\theta)=\dfrac{d\vec{v}}{d\theta}
=\langle -4\cos\theta,-4\sin\theta,0\rangle
\]
The jerk is:
\[
\vec\jmath(\theta)=\dfrac{d\vec{a}}{d\theta}
=\langle 4\sin\theta,-4\cos\theta,0\rangle
\]
Calculate the velocity, acceleration, and jerk for the Helix \(\vec{r}(\theta)=\langle 4\cos\theta,4\sin\theta,3\theta\rangle\).
Position:
\(\vec{r}(\theta)
=(4\cos\theta,4\sin\theta,3\theta)\)
Velocity:
\(\vec{v}(\theta)=\dfrac{d\vec{r}}{d\theta}
=\langle -4\sin\theta,4\cos\theta,3\rangle\)
Acceleration:
\(\vec{a}(\theta)=\dfrac{d\vec{v}}{d\theta}
=\langle -4\cos\theta,-4\sin\theta,0\rangle\)
Jerk:
\(\vec\jmath(\theta)=\dfrac{d\vec{a}}{d\theta}
=\langle 4\sin\theta,-4\cos\theta,0\rangle\)
The position is:
\[
\vec{r}(\theta)=(4\cos\theta,4\sin\theta,3\theta)
\]
We differentiate three times:
The velocity is:
\[
\vec{v}(\theta)=\dfrac{d\vec{r}}{d\theta}
=\langle -4\sin\theta,4\cos\theta,3\rangle
\]
The acceleration is:
\[
\vec{a}(\theta)=\dfrac{d\vec{v}}{d\theta}
=\langle -4\cos\theta,-4\sin\theta,0\rangle
\]
The jerk is:
\[
\vec\jmath(\theta)=\dfrac{d\vec{a}}{d\theta}
=\langle 4\sin\theta,-4\cos\theta,0\rangle
\]
Calculate the velocity, acceleration, and jerk for the Twisted Cubic \(\vec{r}(t)=\left(t,t^2,\dfrac{2}{3}t^{3}\right)\).
Position:
\(\vec{r}(t)
=\left(t,t^2,\dfrac{2}{3}t^{3}\right)\)
Velocity:
\(\vec{v}(t)=\dfrac{d\vec{r}}{dt}
=\langle 1,2t,2t^2\rangle\)
Acceleration:
\(\vec{a}(t)=\dfrac{d\vec{v}}{dt}
=\langle 0,2,4t\rangle\)
Jerk:
\(\vec\jmath(t)=\dfrac{d\vec{a}}{dt}
=\langle 0,0,4\rangle\)
The position is:
\[
\vec{r}(t)=\left(t,t^2,\dfrac{2}{3}t^{3}\right)
\]
We differentiate three times:
The velocity is:
\[
\vec{v}(t)=\dfrac{d\vec{r}}{dt}
=\langle 1,2t,2t^2\rangle
\]
The acceleration is:
\[
\vec{a}(t)=\dfrac{d\vec{v}}{dt}
=\langle 0,2,4t\rangle
\]
The jerk is:
\[
\vec\jmath(t)=\dfrac{d\vec{a}}{dt}
=\langle 0,0,4\rangle
\]
Heading
Placeholder text: Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum Lorem ipsum